多目标优化问题 | Pareto前沿
🔑多目标优化问题详解及帕累托最优
💡美赛第一天选择的题目有关多目标优化,可能会用到这个算法,无论如何先记录一下
💡前言
生活中的优化问题很多,优化问题存在的优化目标超过一个并需要同时处理 ,就成为多目标优化问题
一般情况下 ,多目标优化问题的各个子目标之间是矛盾的,需要进行进行协调和折中处理
其与单目标优化问题的本质区别在于 ,它的解并非唯一 ,而是存在一组由众多 Pareto最优解组成的最优解集合 ,集合中的各个元素称为 Pareto最优解或非劣最优解
💡多目标规划
多目标规划问题是指在多个目标函数之间存在冲突或矛盾的优化问题
一般步骤如下:
- 定义问题的决策变量和目标函数。决策变量是影响问题结果的变量,而目标函数是需要最小化或最大化的问题指标。
- 根据实际问题的特点,确定问题的约束条件。约束条件通常包括等式约束和不等式约束,用于限制决策变量的取值范围。
- 建立多目标规划模型。根据实际问题的特点,选择适当的多目标规划方法,例如线性规划、非线性规划、整数规划等。
💡权重法
权重法(Weighted Sum Method):将多目标问题转化为单目标问题,将多个目标函数加权求和,然后对单个目标函数进行最优化求解。
💡向量优化法
向量优化法是用于解决多目标规划问题的一种方法,它通过将多个目标函数组合成一个目标向量,然后利用向量之间的比较进行求解。向量优化法的基本思想是将多个目标函数的最小化问题转化为一个目标向量的最小化问题。
💡约束优化法
约束优化法是一种常用的求解多目标规划问题的方法,它将目标函数最小化的问题转化为一个带有约束条件的最优化问题。该方法通常可以用来解决复杂的多目标规划问题,其中目标函数之间存在相互制约的关系。
💡帕累托最优
解A优于解B(解A强帕累托支配解B)
假设现在有两个目标函数,解A对应的目标函数值都比解B对应的目标函数值好,则称解A比解B优越,也可以叫做解A强帕累托支配解B
下图解E优于解C,D
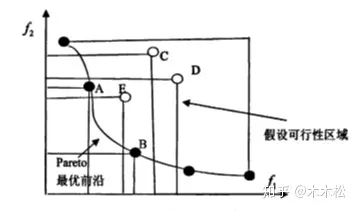
解A无差别于解B(解A能帕累托支配解B)
同样假设两个目标函数,解A对应的一个目标函数值优于解B对应的一个目标函数值,但是解A对应的另一个目标函数值要差于解B对应的一个目标函数值,则称解A无差别于解B,也叫作解A能帕累托支配解B,
上面的图,点C和点D就是这种情况,C点在第一个目标函数的值比D小,在第二个函数的值比D大。
最优解
假设在设计空间中,解A对应的目标函数值优越其他任何解,则称解A为最优解
实际生活中这种解是不可能存在的,由此提出了帕累托最优解
帕累托最优解
假设两个目标函数,对于解A而言,在 变量空间 中找不到其他的解能够优于解A(注意这里的优于一定要两个目标函数值都优于A对应的函数值),那么解A就是帕累托最优解
下图x1 x2之间都是帕累托最优解
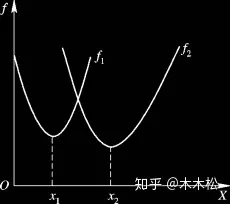
帕累托最优前沿
帕累托最优解对应的目标函数值就是帕累托最优前沿
0204更
哎呦最后竟然真的用到了pareto!
下面是算法伪代码,板子上写不出好看的字
